next to Subtractor
Adder
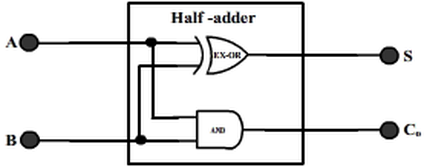
Addition is simplest arithmetic operation. In digital, simplest addition would be addition of two single-bit numbers. The logic circuitry that performs this operation is known as half adder.
Inputs to the half adder are two single-bit numbers, say A and B. Thus, there are four possible combinations of these two inputs. And the is output sum of them, say S. The truth table that follows shows the addition:
Inputs to the half adder are two single-bit numbers, say A and B. Thus, there are four possible combinations of these two inputs. And the is output sum of them, say S. The truth table that follows shows the addition:
When both bits are logic 1, then addition result is (2)d i.e. (10)b. So, obviously another bit of output is required to represent the addition result. We call this bit the ‘carry out’, usually represented by Co.
Now the new truth table is:
Now the new truth table is:
By inspecting the truth table, we recognize that both sum and carry-out represent standard logic gates viz. EX-OR gate & AND gate respectively.
S = A EX-OR B & Co = A AND B
So here we go with our half adder:
S = A EX-OR B & Co = A AND B
So here we go with our half adder:
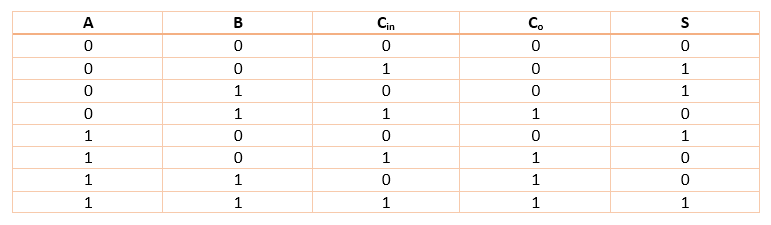
The half adder is able to perform addition of two bits, and provides us with SUM and CARRY. However, in practice we do addition of multi-bit numbers (e.g. 32-bit numbers etc.). In that case, carry may be generated by addition of say nth bit which must be used in addition of (n+1)th bit. The half adder discussed above gives no provision to add the previous carry. That is why it’s termed as HALF adder.
So we need a full-adder. And obviously, it adds two single bit numbers along with previous carry {termed carry-in), and gives sum and carry-out.
Let’s begin with truth table of full adder:
So we need a full-adder. And obviously, it adds two single bit numbers along with previous carry {termed carry-in), and gives sum and carry-out.
Let’s begin with truth table of full adder:
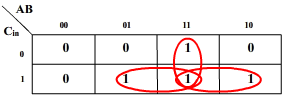
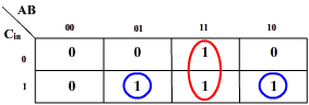
K-map for Co: K-map for S:
Co = AB + BCin + ACin S = A EX-OR B EX-OR Cin
= AB + Cin (A+B)
The expression for S is written directly considering diagonal adjacency between all the prime-implicants. It can also be derived.
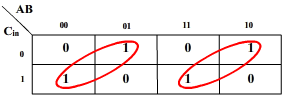
Alternately, the K-map for Co can also be:
= AB + Cin (A+B)
The expression for S is written directly considering diagonal adjacency between all the prime-implicants. It can also be derived.
Alternately, the K-map for Co can also be:
This gives-
Co = AB + CinA’B + CinAB’
“Note that A’ implies A_bar i.e. negation of A”
Thus, Co = AB + Cin (A’B + AB’)
= AB + Cin (A EX-OR B)
This equation differs from prior one in that OR between A and B is replaced by EX-OR. It just a matter of choice which gate to use for implementation. Either implementation gives same result.
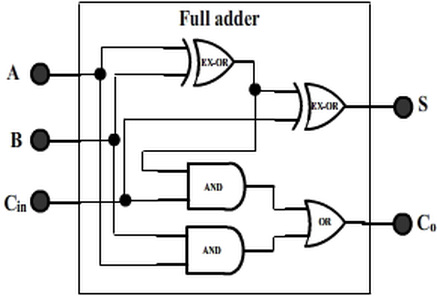
The logic circuitry we have come across now is illustrated below:
Co = AB + CinA’B + CinAB’
“Note that A’ implies A_bar i.e. negation of A”
Thus, Co = AB + Cin (A’B + AB’)
= AB + Cin (A EX-OR B)
This equation differs from prior one in that OR between A and B is replaced by EX-OR. It just a matter of choice which gate to use for implementation. Either implementation gives same result.
The logic circuitry we have come across now is illustrated below:
Take some time to see which wire goes to which connection, and it should match the equations discussed above!
BCD Adder
BCD is shorthand of Binary Coded Decimal. A BCD number is binary representation of a decimal number digit-by-digit.
e.g. Decimal number (307)d in binary is (1 0011 0011)b.
the same in BCD is (0011 0000 0111)BCD
i.e. 3, 0 and 7 are represented in binary separately.
BCD adder, is in turn, the adder which adds two BCD numbers. This is useful when we input numbers in decimal form and want result to be displayed in decimal form, although all the internal computation is on binary numbers.
Now that we already have designed binary adder, all we need to do is to develop some logic to convert this natural binary result into BCD number.
Let P and Q are the two BCD numbers we want to add, both of which can range from (0)d to (9)d. So, the addition result must be in the range (0)d to (18)d. And this result is to be converted from binary to BCD.
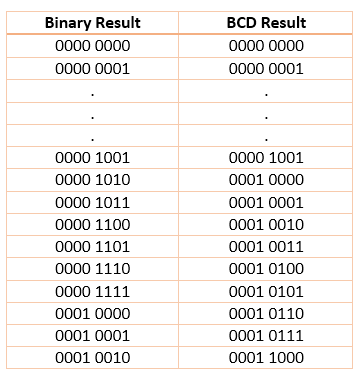
Truth table for BCD addition result:
e.g. Decimal number (307)d in binary is (1 0011 0011)b.
the same in BCD is (0011 0000 0111)BCD
i.e. 3, 0 and 7 are represented in binary separately.
BCD adder, is in turn, the adder which adds two BCD numbers. This is useful when we input numbers in decimal form and want result to be displayed in decimal form, although all the internal computation is on binary numbers.
Now that we already have designed binary adder, all we need to do is to develop some logic to convert this natural binary result into BCD number.
Let P and Q are the two BCD numbers we want to add, both of which can range from (0)d to (9)d. So, the addition result must be in the range (0)d to (18)d. And this result is to be converted from binary to BCD.
Truth table for BCD addition result:
This table shows that for binary result from (0000 0000)b to (0000 1001)b, no conversion is needed; but after that, we need extra logic for conversion.
Instead of drawing K-map for each of BCD result bit, just by inspecting truth table we see that extra (6)d is added to the binary result, when it exceeds (9)d to get the BCD result. Moreover, there are following three conditions under which (6)d must be added to the result:
(i) The bit-1 and bit-3 (starting from bit-0), are binary 1, OR
(ii) The bit-1 and bit-2 are binary 1, OR
(iii) There is carry generated from lower nibble to higher nibble.
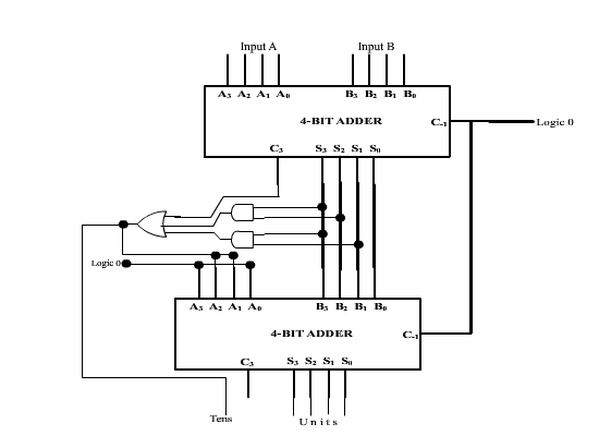
So, BCD adder is natural-binary adder along with an extra adder as illustrated below:
Instead of drawing K-map for each of BCD result bit, just by inspecting truth table we see that extra (6)d is added to the binary result, when it exceeds (9)d to get the BCD result. Moreover, there are following three conditions under which (6)d must be added to the result:
(i) The bit-1 and bit-3 (starting from bit-0), are binary 1, OR
(ii) The bit-1 and bit-2 are binary 1, OR
(iii) There is carry generated from lower nibble to higher nibble.
So, BCD adder is natural-binary adder along with an extra adder as illustrated below: