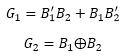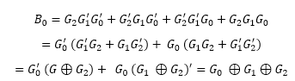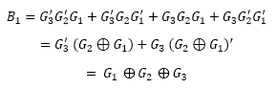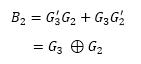Code Converters
Numbers are usually coded in one form or another so as to represent or use it as required. For instance, a number ‘nine’ is coded in decimal using symbol (9)d. Same is coded in natural-binary as (1001)b. While digital computers all deal with binary numbers, there are situations wherein natural-binary representation of numbers in in-convenient or in-efficient and some other (binary) code must be used to process the numbers.
One of these other code is gray-code, in which any two numbers in sequence differ only by one bit change. This code is used in K-map reduction technique. The advantage is that when numbers are changing frequently, the logic gates are turning ON and OFF frequently and so are the transistors switching which characterizes power consumption of the circuit; since only one bit is changing from number to number, switching is reduced and hence is the power consumption.
Let’s discuss the conversion of various codes from one form to other.
One of these other code is gray-code, in which any two numbers in sequence differ only by one bit change. This code is used in K-map reduction technique. The advantage is that when numbers are changing frequently, the logic gates are turning ON and OFF frequently and so are the transistors switching which characterizes power consumption of the circuit; since only one bit is changing from number to number, switching is reduced and hence is the power consumption.
Let’s discuss the conversion of various codes from one form to other.
Binary-to-Gray
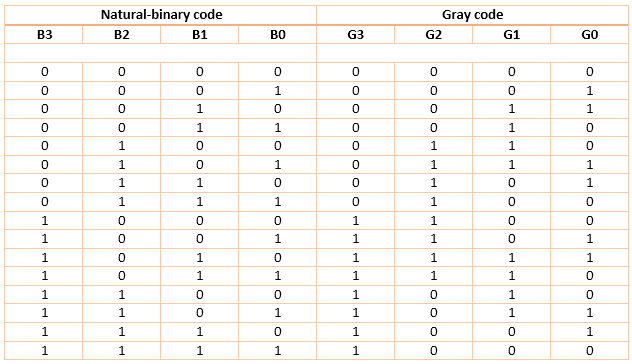
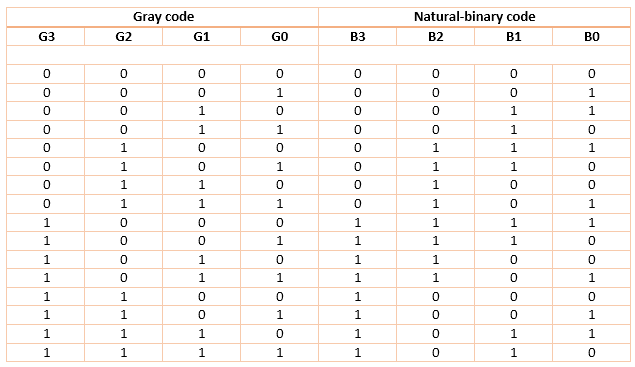
The table that follows shows natural-binary numbers (upto 4-bit) and corresponding gray codes.
Looking at gray-code (G3G2G1G0), we find that any two subsequent numbers differ in only one bit-change.
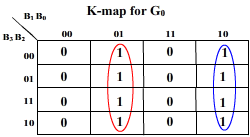
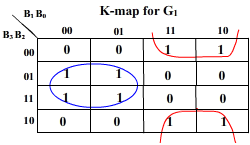
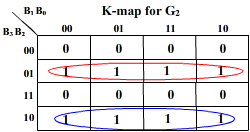
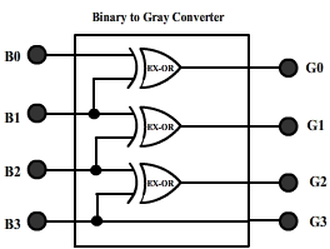
The same table is used as truth-table for designing a logic circuitry that converts a given 4-bit natural binary number into gray number. For this circuit, B3 B2 B1 B0 are inputs while G3 G2 G1 G0 are outputs.
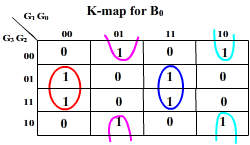
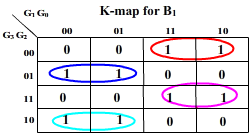
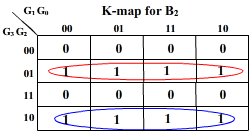
K-map for the outputs:
The same table is used as truth-table for designing a logic circuitry that converts a given 4-bit natural binary number into gray number. For this circuit, B3 B2 B1 B0 are inputs while G3 G2 G1 G0 are outputs.
K-map for the outputs:
And G3 = B3
So that’s a simple three EX-OR gate circuit that converts a 4-bit input binary number into its equivalent 4-bit gray code. It can be extended to convert more than 4-bit binary numbers.
Gray-to-Binary
Once the converted code (now in Gray form) is processed, we want the processed data back in binary representation. So we need a converter that would perform reverse operation to that of earlier converter. This we call a Gray-to-Binary converter.
The design again starts from truth-table:
The design again starts from truth-table:
Then the K-maps:
And B3 = G3
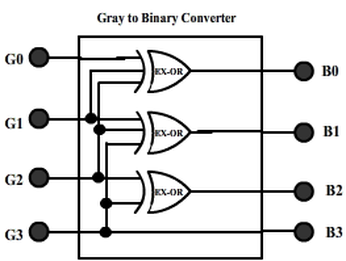
The realization of Gray-to-Binary converter is
The realization of Gray-to-Binary converter is